Concave Mirror: make images interactively and learn
Link for interactive practice ☝
Sampling: analog to digital converter
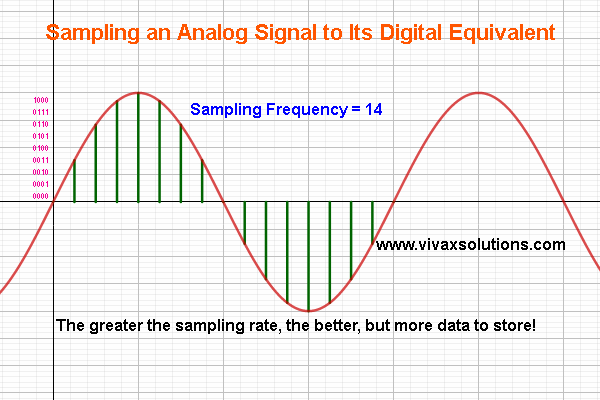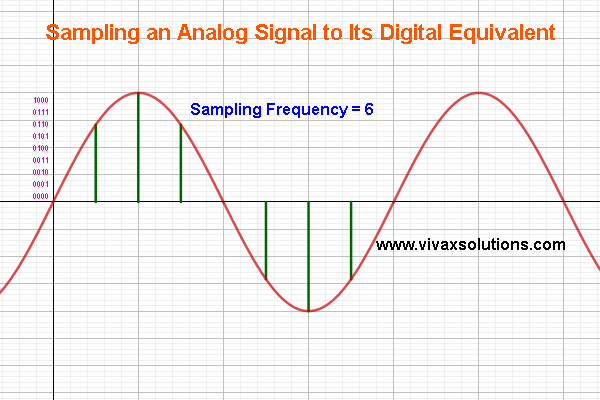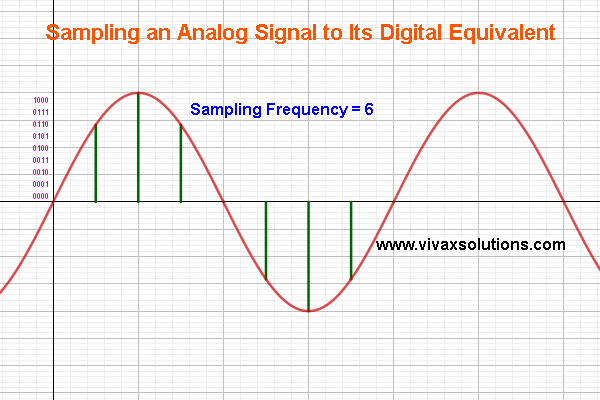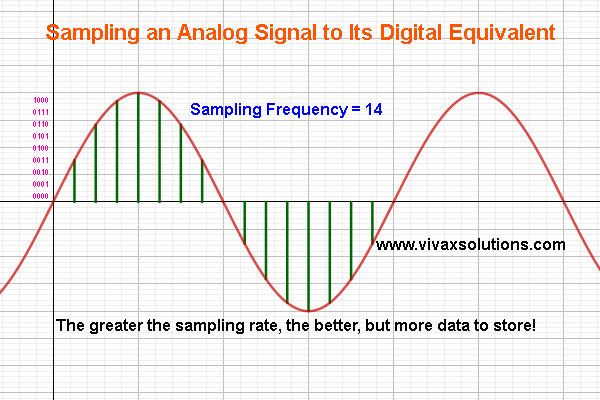 |
| Analog to digital conversion |
Potentiometer
 |
| Potentiometer |
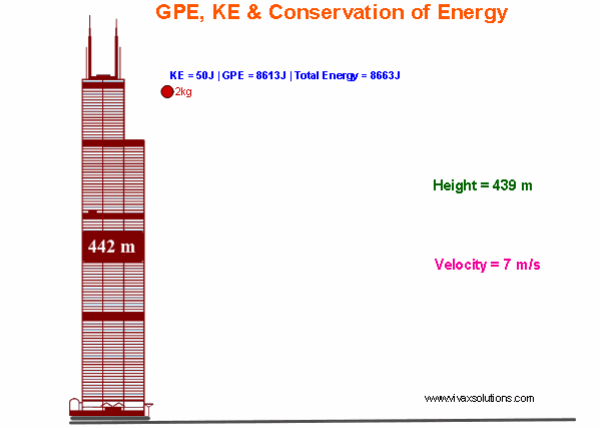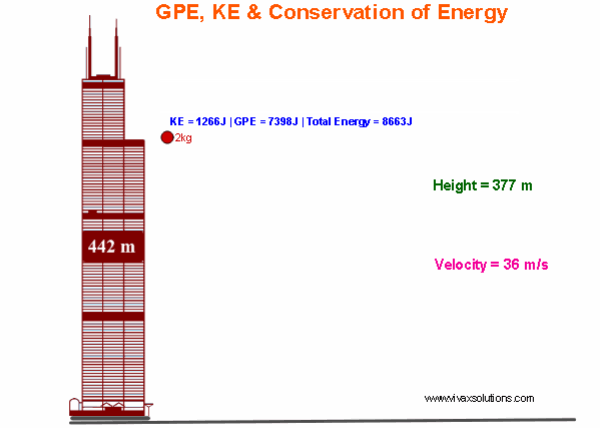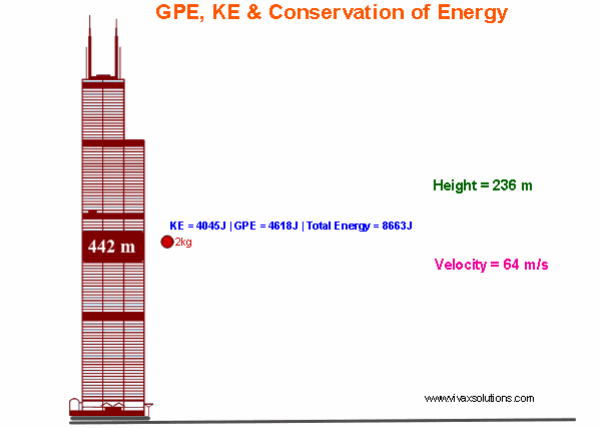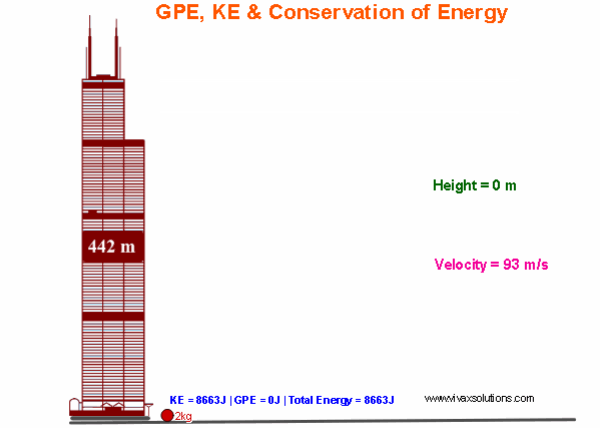
The Conservation of Mechanical Energy: GPE to KE
Displacement vs Distance
 |
| Distance vs displacement |
Link for interactive practice ☝
The Minimum Height of a Mirror
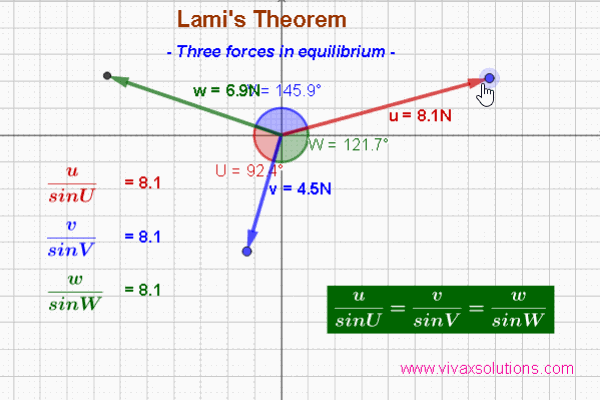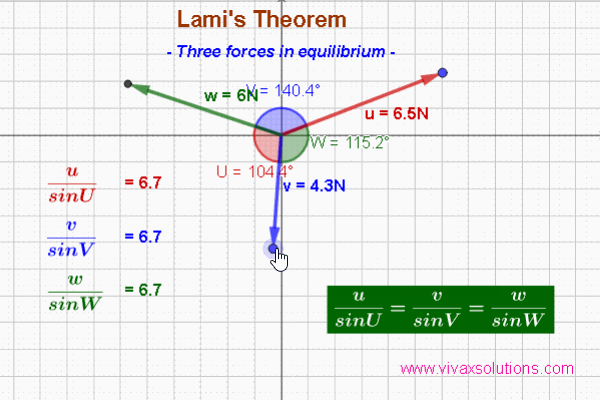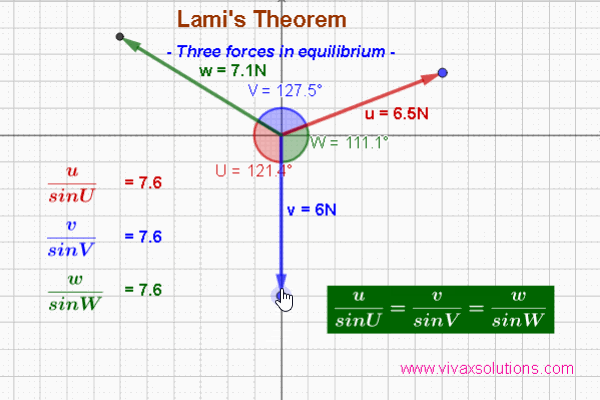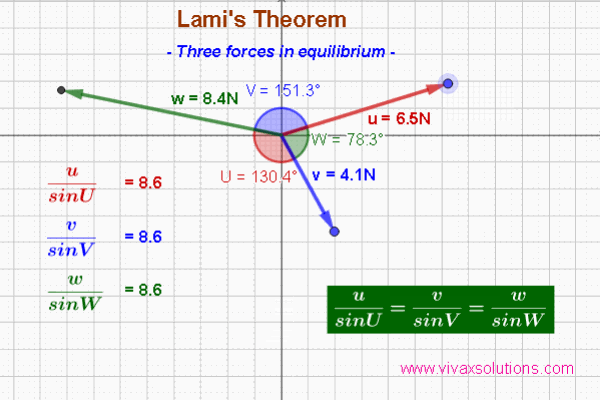
The Lami's Theorem
Link for interactive practice ☝
Newton's First and Second Law of Motion
Link for interactive practice ☝
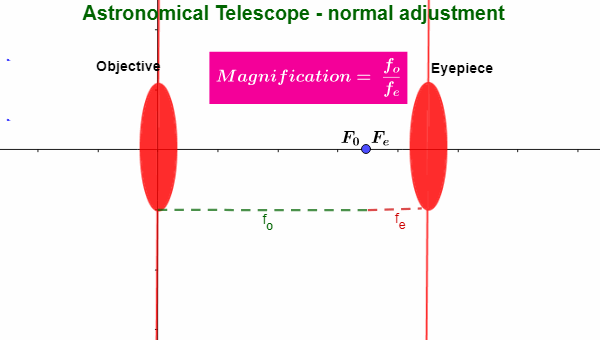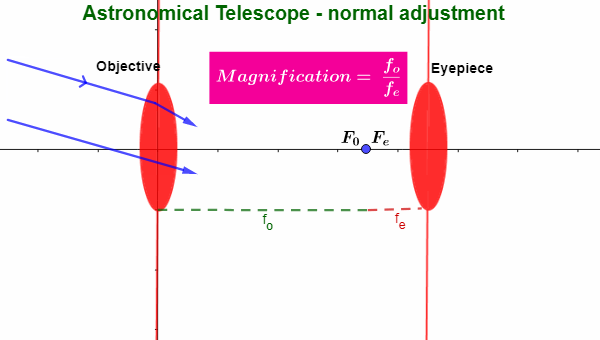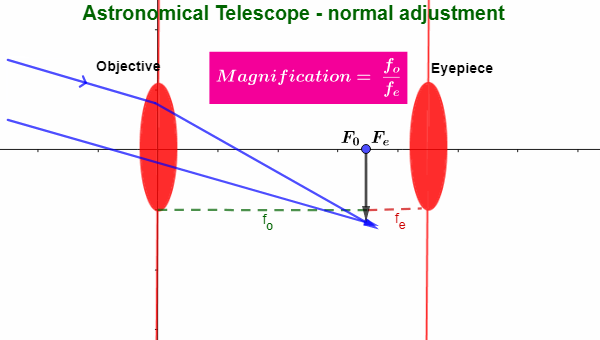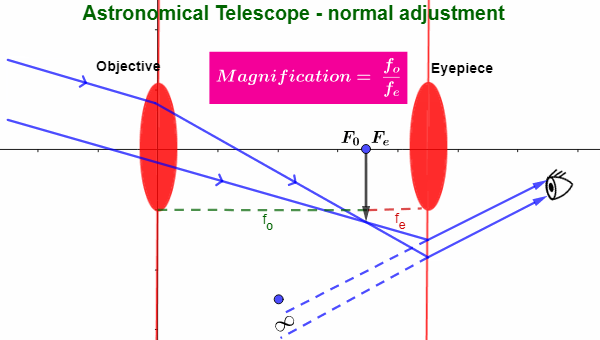
Astronomical Telescope
Link for interactive practice ☝
Link for interactive practice ☝
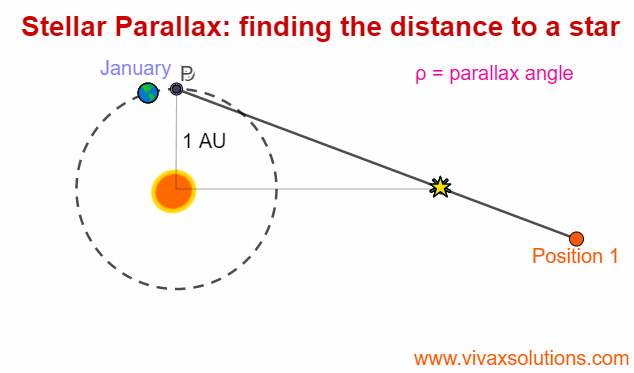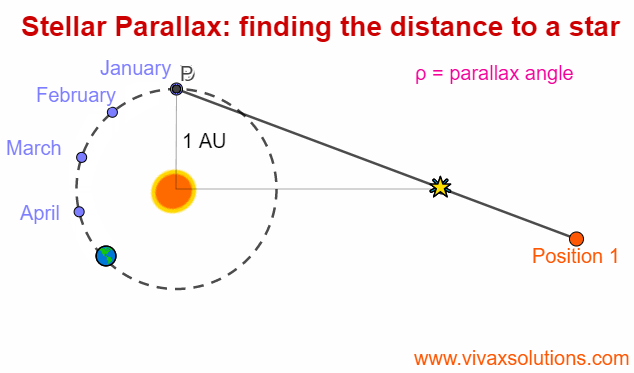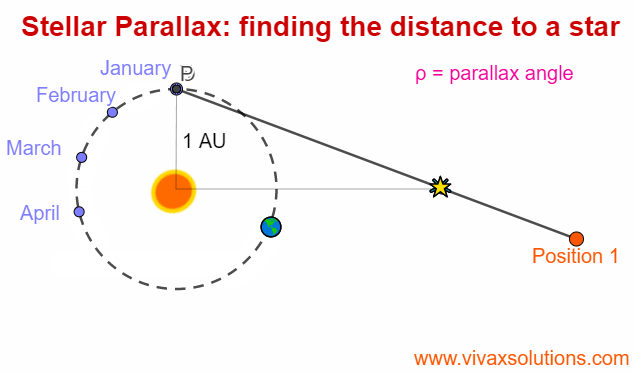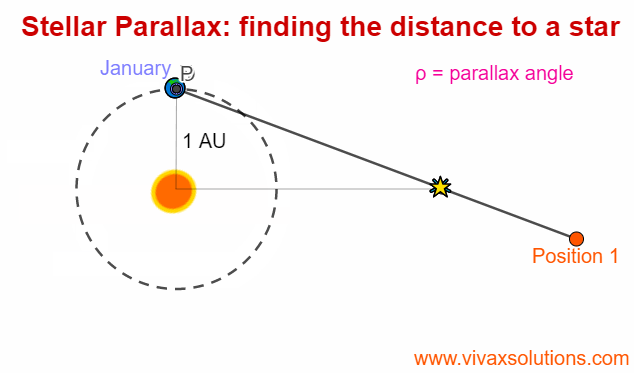
Stellar Parallax
Resistors in Series and Parallel - simulator
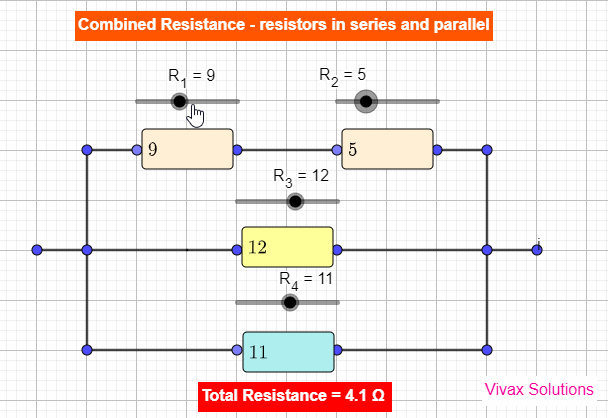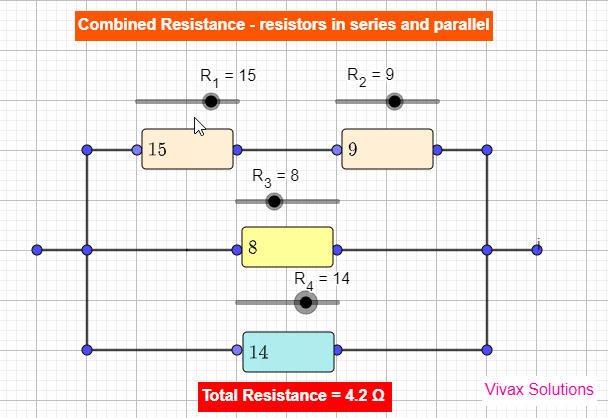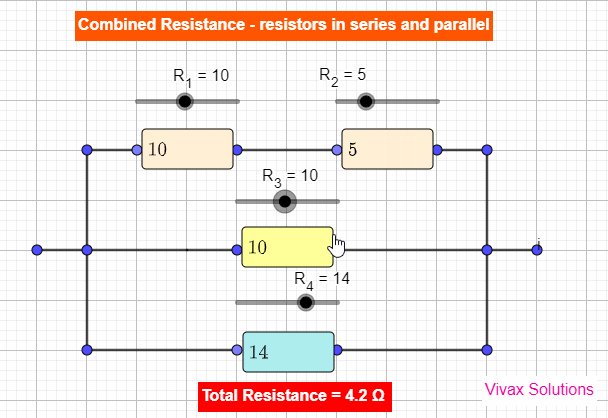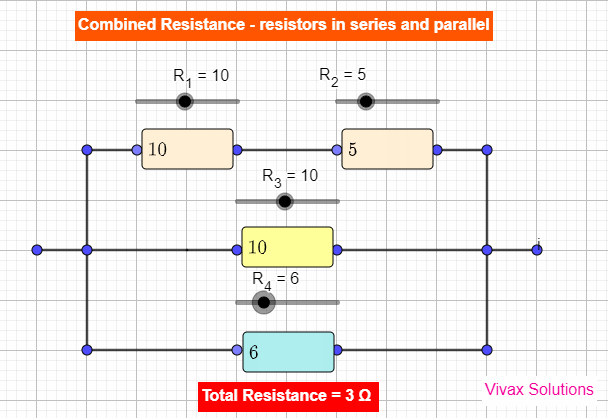 |



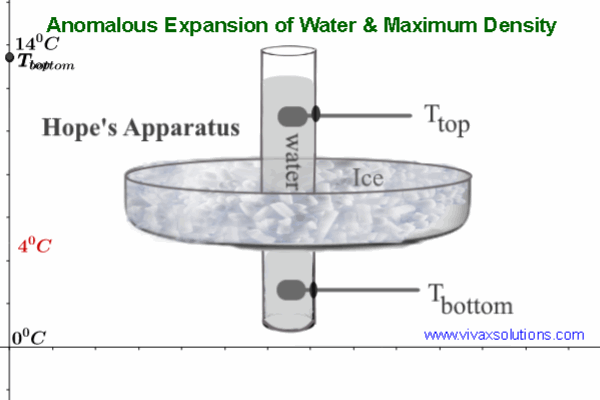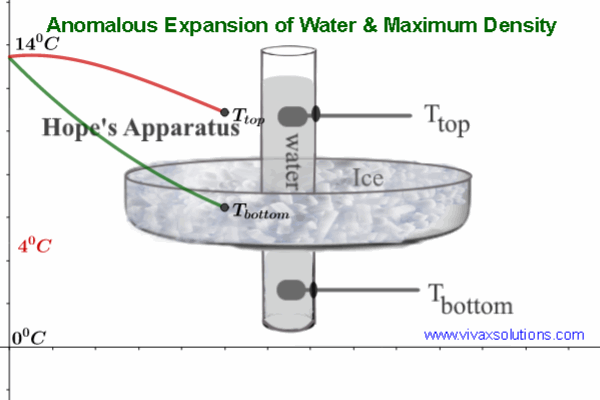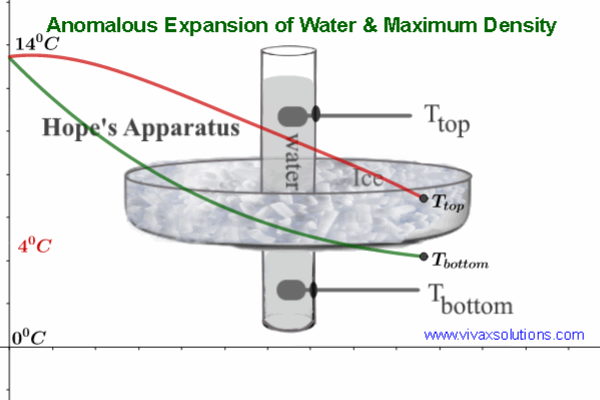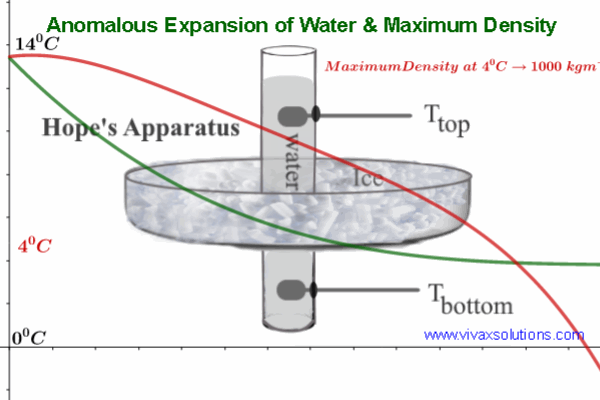







0 comments:
Post a Comment