Differentiation: problem solving

Snell's Law When light refracts from one medium to another, the ratio of sine of the angles is equal to the ratio of refractive index of each corresponding medium. Snell's Law implies that light, when refracting from one medium to another, takes the shortest path. We can show by differentiatio…

Read more »

Pascal's Triangle in Python for Computer Science: GCSE, IGCSE and A Level

The above simulation is produced in Python with aid of three functions. They are as follows: Factorial function  A function to generate combinations - nCr A function to produce the Pascal's Triangle You can practise it interactively with the following simulation. Please make sure you keep the number…

Read more »

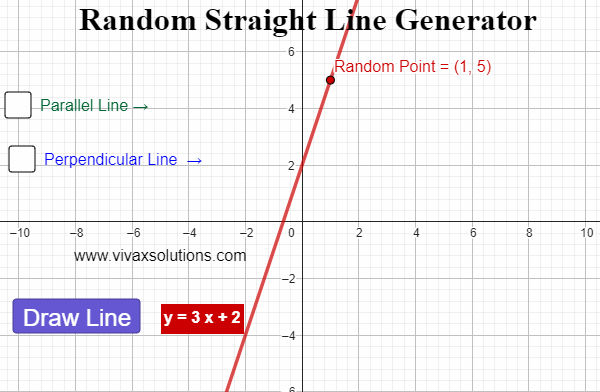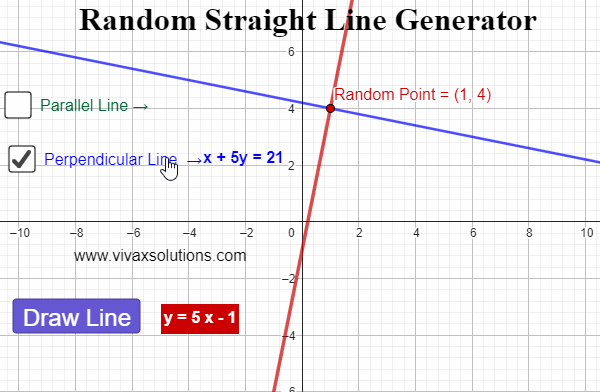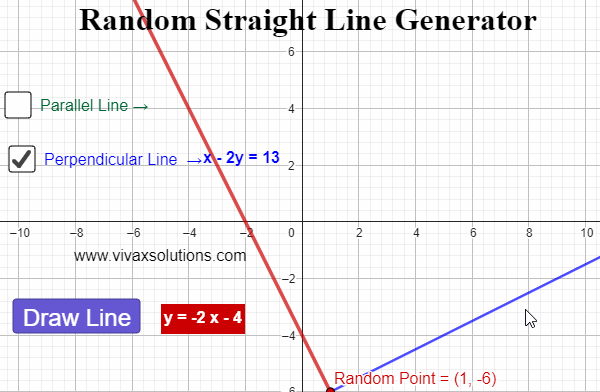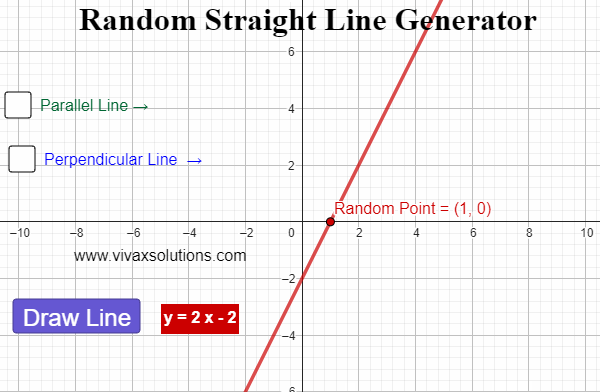
Straight Line Graph Generator for Maths Teachers: GCSE, IGCSE, GCE O Level, GCE A Level, A Level

Created with GeoGebra, this applet lets you generate straight line graphs at random, displaying the corresponding equation for each. In addition, you can find a parallel line - and its equation - for each line. Moreover, for each generated line, a random point is created. Then, the perpendicular line…

Read more »

Creating Pascal's Triangle in C#: for computer science at GCSE, IGCE, A Level and programmers

The above animation is produced in C# programming language for students who do computer science at GCSE, IGCSE, IB and A Level. The code snippet consists of four major function that collectively produce the Pascal's Triangle. They are: A factorial function A function to generate combinations A funct…

Read more »

Straight Line Graph Generator: for Year 9, GCSE Maths

The equation of a straight line is given by the formula, y = mx + c, where m and c are the gradient and intercept respectively. The gradient, m, is the slope or steepness of the line; the intercept, c, is the point where it crosses the y-axis at. E.g. A straight line passes through (1,2) and (3, 8). F…

Read more »

Constructions for Maths: GCSE, IGCSE and GCE - OL

A circumcircle is a circle that touches the three vertices of a circle from outside. It can easily be constructed by the following steps: Construct the perpendicular bisectors of each side of the triangle Locate the point of intersection of the bisectors The point of intersection is the centre of the c…

Read more »

Correlation and the Line of Best Fit - for GCSE, IGCSE and A-Level Maths

The above animation shows how a code snippet written in JavaScript determines the line of best fit for an evolving set of data. The line is drawn accurately while performing the mathematical requirements for it to be accurate and minimizing the known errors. This is a stepping stone to AI - Artificial…

Read more »

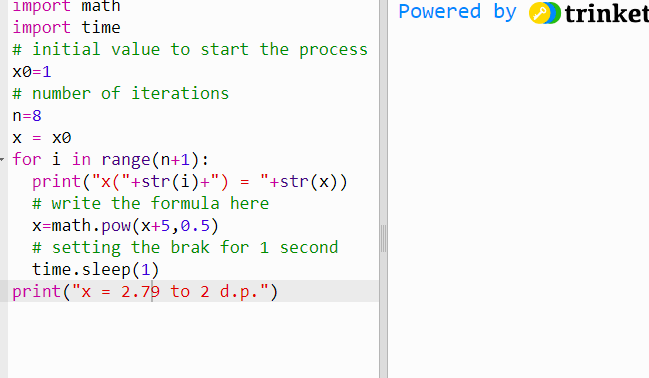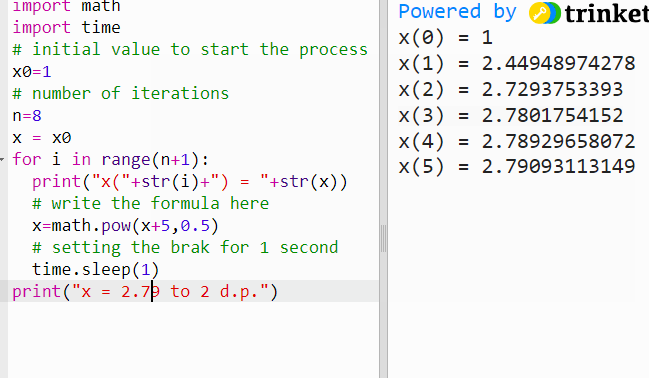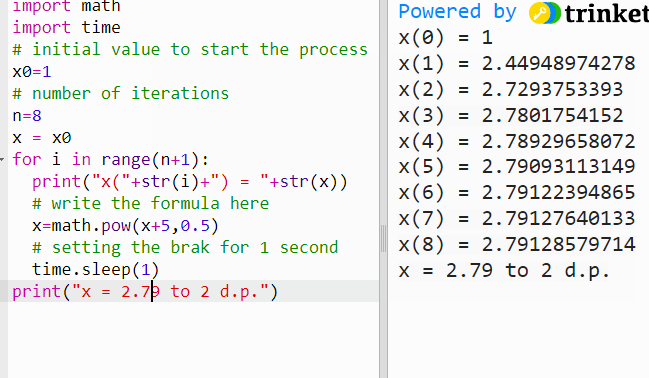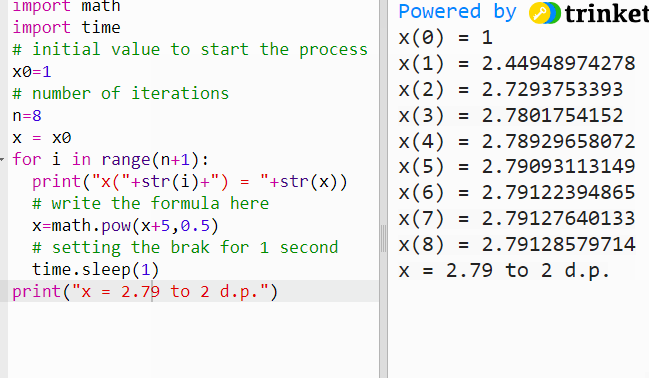
Solving equations by iteration - GCSE, IGCSE and A Level maths - using Python

Iteration If f(x) =0, it can be rearranged in the form of x = g(x), where both f(x) and g(x) are functions of x. Then x = g(x) is said to be in iterative form. E.g. x² - x - 5 = 0 x² = x + 5 x n+1 = √(x n + 5) - f(x) = 0 in iterative form If x n is known, x n+1 can be calculated. The above is not the only ite…

Read more »

How to measure atmospheric pressure by a mercury barometer - a toxic legacy!

The pressure of a liquid column is given by the formula, p = hdg, where h, d and g are the depth/height, density and the acceleration due to gravity respectively.  A few decades ago, in order to measure the atmospheric pressure, a simple barometer was used. It consisted of a thin, long, glass tube -…

Read more »

Differentiating Trigonometric Functions

When it comes to differentiating the functions of sin x and cos x, we need to use two fractions of the functions in question, when the variable approaches zero must be considered. They are as follows: lim sin (x) / x, as x → 0 lim (cos x - 1) / x as x → 0 Based on the above, sin x and cos x can be dif…

Read more »

Verification of the area of a circle

The proof with the aid of parametric equation is as follows:

Read more »

Energy changes in simple harmonic motion

The above simulation of the simple harmonic motion involving a pendulum shows how the potential energy, PE and kinetic energy, KE, change with the position of the pendulum, provided that the latter swings through a small angle. As you can see the total energy of the system remains the same: the loss…

Read more »

Simple Harmonic Motion of Pendulum

The above simulation shows how the angle of oscillation determines the validity of the formula of the simple pendulum. During the process of deriving the formula, we assume the angle is small and measured in radians.  For the full tutorial, please follow this link .

Read more »

A Level further maths: equation of a half line - complex numbers

The following simulation, which is fully interactive, shows you how to  derive the equation of a half line . A half line , by definition,  is a line that stretches from a point in one direction up to infinity.  You may change the position of the arbitrary point, denoted by Z, and the equation of the hal…

Read more »

Locus of a point: A Level further maths - complex numbers

With the following simulation, you can find out the equation of the locus of a point that moves in such a way that Argument(Z - z1) = Θ. The locus of the point is a half line - a line that starts from a point and moves only in one direction from it up to infinity.  You can change the position of Z - …

Read more »

Resultant Moment of Forces - GCSE, IGCSE and A Level physics

With the following simulation, you can practise the moment of forces interactively. Moment of a force = force X perpendicular distance from the pivot The resultant moment or the total moment is the algebraic sum of the moments  of forces.  In the simulation, the clockwise moment is considered as posit…

Read more »

A Level Core Maths: complex numbers and loci

The above simulation can be used to learn the locus of a point, under given conditions. Just move the point, Z, using the mouse and watch the appearance and disappearance of the shaded region. Alternatively, you can use the play button at the bottom-right corner too.

Read more »

Timed Multiple Choice Question Test for A Level Physics - Capacitors: AQA, OCR, Edexcel

Multiple Choice Questions - A Level Physics - Capacitors - Master capacitor concepts with this interactive A Level Physics quiz! Whether you're an OCR, AQA, or Edexcel student, this multiple-choice question format is designed to challenge your understanding of capacitors. Key topics covered: Cap…

Read more »

Master A-Level Computer Science Python with our Interactive Quiz!

Time: 15 minutes Created and Programmed  by Vivax Solutions Master A-Level Computer Science Python with our Interactive Quiz! **Struggling to revise for your A-Level Computer Science exams?** Test and solidify your Python knowledge with our comprehensive multiple-choice quiz! This interactive tool caters…

Read more »