Iteration for A Level Maths: staircase method & cobweb method

E.g. f(x) = x² - x - 4 When the above is rearranged in the form of x = g(x), it is said to be in iterative form. x² - x - 4 = 0 x = 1 + x/4 x n+1 = 1 + x n / 4 If x n is known, x n+1 can be calculated. The initial value to trigger off the iterative process is found by looking for change in sign of…

Read more »

Mechanics - A Level Applied Maths & Physics: really challenging questions

An object that falls off a tree travels 16/25 th of the height of the tree during the last second. Assuming that g = 10 m/s², find the total time taken for the fall and the height of the tree. A balloon is steadily rising at 5 m/s. After 4 seconds of its motion, a nail from the balloon falls off. Sk…

Read more »

Basic Integration: finding the area under a curve by a GeoGebra applet - fully interactive

With the following GeoGebra applet, you can find out the area under a curve by integration -  interactively.  All you need to do is  to move the two sliders to points of your choice and tick the checkbox for answer to appear. The function used in this case is a quadratic function. Enjoy, learn and pro…

Read more »

Linear and Geometric Sequences for GCSE, IGCSE & A Level

E.g.1 : Find the nth term of the sequence: 3, 7, 11, 15, ... The common difference is 4.  Let N = an + b, where N is the nth term and a an b are constants to be found. 3 = a(1) + b = a + b 7 =  a(2) + b = 2a + b Solving the two equations simultaneously, we get a = 4 and b = -1 So, the nth term, N = 4n - 1 …

Read more »

A Level Further Maths: Simple Harmonic Motion - SHM: Light Damping

The following example shows how to model light damping by using a second order differential equation. The second-order differential equation modelling light damping is given by: \[ \ddot{x} + 0.5 \dot{x} + 4 x = 0 \] The characteristic equation is: \[ m^2 …

Read more »

A Level Further Maths: Demystifying Polar Coordinates through Shapes

The above shape is known as cardioid in mathematics. It is produced by the polar equation, r = a(1 + cos(Θ)), where a can be an integer. You can practise a cardioid with the following simulation and see how r and Θ do the magic to produce the shape. Rose Petals You can practise the creation of shapes …

Read more »

The exponential graph

The exponential function is a special exponential function; the gradient of any point on the curve is the same as the value of the function at that point.

Read more »

Concave, convex functions and points of inflection

Concave functions If f''(x) ≤ 0 in a given interval of x, the function is said to be concave. Convex functions If f''(x) ≥ 0 in a given interval of x, the function is said to be convex. Point of Inflection The point at which a curve changes being concave to convex or vice versa is called…

Read more »

Differentiation: problem solving

Snell's Law When light refracts from one medium to another, the ratio of sine of the angles is equal to the ratio of refractive index of each corresponding medium. Snell's Law implies that light, when refracting from one medium to another, takes the shortest path. We can show by differentiatio…

Read more »

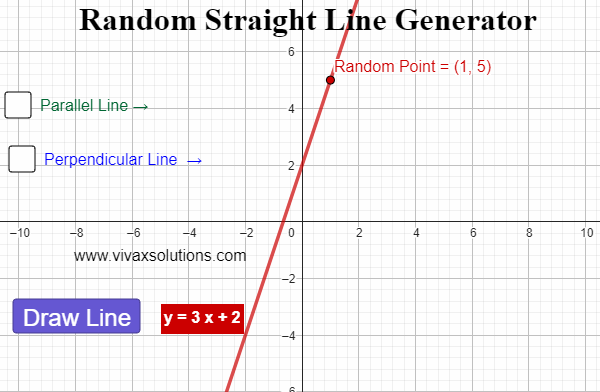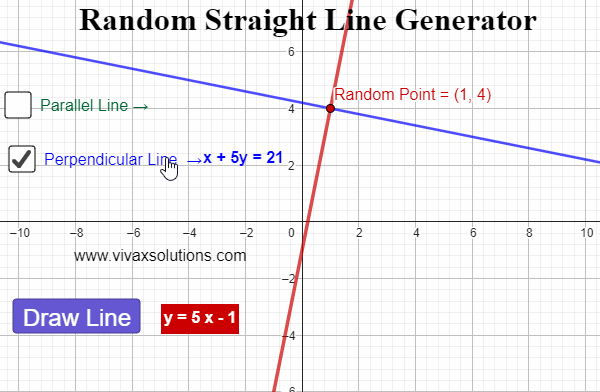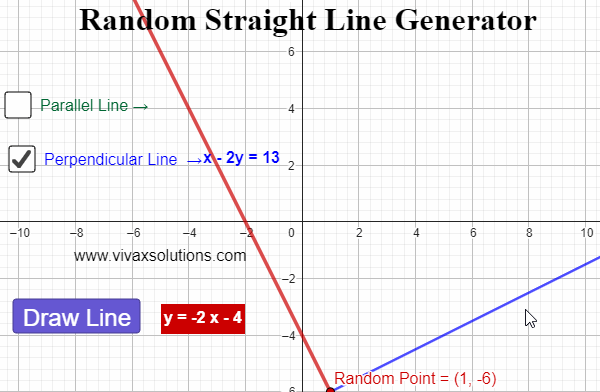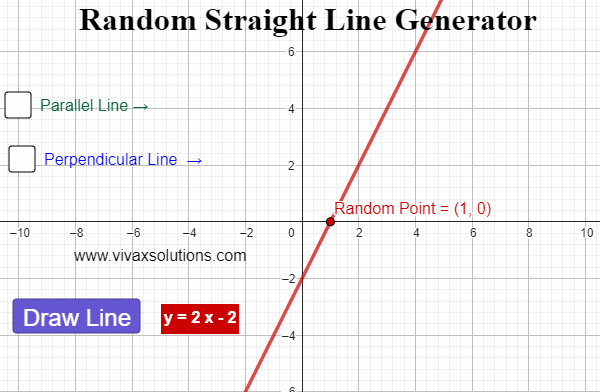
Straight Line Graph Generator for Maths Teachers: GCSE, IGCSE, GCE O Level, GCE A Level, A Level

Created with GeoGebra, this applet lets you generate straight line graphs at random, displaying the corresponding equation for each. In addition, you can find a parallel line - and its equation - for each line. Moreover, for each generated line, a random point is created. Then, the perpendicular line…

Read more »

Correlation and the Line of Best Fit - for GCSE, IGCSE and A-Level Maths

The above animation shows how a code snippet written in JavaScript determines the line of best fit for an evolving set of data. The line is drawn accurately while performing the mathematical requirements for it to be accurate and minimizing the known errors. This is a stepping stone to AI - Artificial…

Read more »

Differentiating Trigonometric Functions

When it comes to differentiating the functions of sin x and cos x, we need to use two fractions of the functions in question, when the variable approaches zero must be considered. They are as follows: lim sin (x) / x, as x → 0 lim (cos x - 1) / x as x → 0 Based on the above, sin x and cos x can be dif…

Read more »

Verification of the area of a circle

The proof with the aid of parametric equation is as follows:

Read more »

A Level further maths: equation of a half line - complex numbers

The following simulation, which is fully interactive, shows you how to  derive the equation of a half line . A half line , by definition,  is a line that stretches from a point in one direction up to infinity.  You may change the position of the arbitrary point, denoted by Z, and the equation of the hal…

Read more »

Locus of a point: A Level further maths - complex numbers

With the following simulation, you can find out the equation of the locus of a point that moves in such a way that Argument(Z - z1) = Θ. The locus of the point is a half line - a line that starts from a point and moves only in one direction from it up to infinity.  You can change the position of Z - …

Read more »

A Level Core Maths: complex numbers and loci

The above simulation can be used to learn the locus of a point, under given conditions. Just move the point, Z, using the mouse and watch the appearance and disappearance of the shaded region. Alternatively, you can use the play button at the bottom-right corner too.

Read more »

Modelling with Differentiation for A Level Maths and Physics

The motion of an object under gravity can easily be modelled by differentiation. Suppose the motion of a stone is given by the formula, y = 16t - 4t 2 , where y and t are displacement and time respectively.  y = 16t - 4t 2 dy/dt = 16 - 8t When the stone reaches the highest point, dy/dt = 0 16 - 8t = 0 8t = …

Read more »

The dot product of two vectors: for A Level Further Maths

The dot product or scaler product of two vectors, a and b, is defined as follows: a.b = |a| |b| cos θ Since |a|, |b| and cos t are scalers, the dot product is a scaler. The dot product of unit vectors i.i = |i| |i| cos 0 = 1 X 1 X 1 = 1 i.j = |i| |j| cos 90 = 1 X 1 X 0 = 0 j.j = |j| |j| cos 0 = 1 X 1 X 1…

Read more »