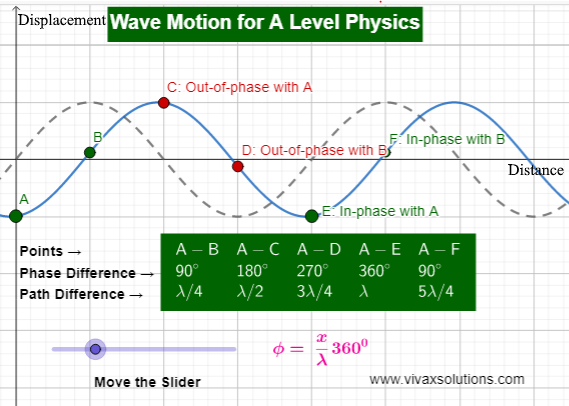
In the above animation, five points on the wave are considered for the explanation.
The fully interactive applet is given below for you to practise.
The phase of a point implies its direction of vibration on a wave. For example, both points A and E vibrate exactly the same way are said to be in phase: when A goes up so does B; the phase difference is either 00 or 3600.
If you consider the motion of points A and C, on the other hand, when A goes down C goes up or vice versa. Therefore, A and C are said to be out of phase; the phase difference is 1800.
That means the phase difference between two points on a wave - or two waves for that matter - can take any value between 00 and 3600.
The phase difference between points A and B, for instance, is 900.
From the above examples, it is clear there is a connection between the path difference between two points - or two waves - and phase difference. It is as follows:
Phase difference = (path difference / wavelength) x 360
φ = x/λ X 3600, where x is the distance between two points or waves.
Wave Profile
The snap shot of a wave taken at a given time is called a wave profile. It is the displacement of the particles of a wave against the distance. The following image is a snap shot of the above wave - hence, a wave profile.





nice
ReplyDelete