Multiple Choice Questions - A Level Physics and Mechanics - Time: 40 minutes Created and Programmed by Vivax Solutions Start the Quiz Submit Quiz
Thursday, 28 April 2022
Sunday, 24 April 2022
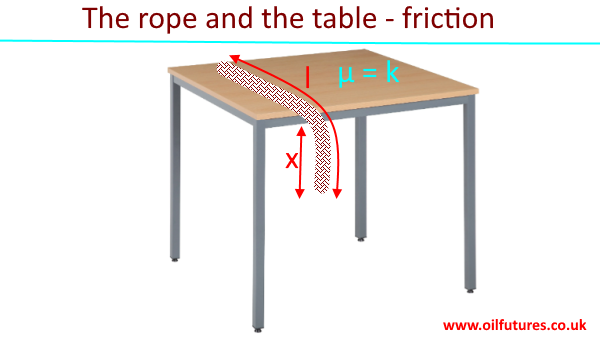
Challenging questions for in friction - for physics and mechanics: A Level and IB
1) If the section of the rope that hangs down is about to move on the table, find and expression for x in terms of the coefficient of friction and the length of the rope. 2) The mass of a book is 2kg and is pressed against a wall by a horizontal force to stop it from sliding down. Find the minimum val…
Saturday, 16 April 2022
Modelling with Differentiation for A Level Maths and Physics
The motion of an object under gravity can easily be modelled by differentiation. Suppose the motion of a stone is given by the formula, y = 16t - 4t 2 , where y and t are displacement and time respectively. y = 16t - 4t 2 dy/dt = 16 - 8t When the stone reaches the highest point, dy/dt = 0 16 - 8t = 0 8t = …
Tuesday, 12 April 2022
The dot product of two vectors: for A Level Further Maths
The dot product or scaler product of two vectors, a and b, is defined as follows: a.b = |a| |b| cos θ Since |a|, |b| and cos t are scalers, the dot product is a scaler. The dot product of unit vectors i.i = |i| |i| cos 0 = 1 X 1 X 1 = 1 i.j = |i| |j| cos 90 = 1 X 1 X 0 = 0 j.j = |j| |j| cos 0 = 1 X 1 X 1…
Saturday, 9 April 2022
Simple Harmonic Motion of a liquid inside a U Tube
The above shows how a column of liquid of density ρ can be made to oscillate while undergoing SHM, simple harmonic motion. When you blow gently into the tube at one end, the excess weight of the column of height, x, pushes the rest of the liquid down with a force that results in an downward accelera…
Friday, 8 April 2022
Challenging questions for A Level Physics
These are some challenging questions that may potentially appear in the forthcoming A Level physics examination : 1) Two masses of 10kg each, are attached to a spring balance that is calibrated in kg . What is the reading of the spring balance, m, if the system is in balance? 2) A boat of length 5m is…
Sunday, 3 April 2022
Chromatic Aberration
When light hits a lens, the components of the light refract through different angles, owing to their unique wavelengths. The blue light, for instance, refracts more than the red light; the wave length of the former is smaller than that of the latter. Due to chromatic aberration, the image formed by …
Subscribe to:
Comments (Atom)
Popular Posts
-
Multiple Choice Questions - A Level Physics and Mechanics - Time: 40 minutes Created and Programmed by Vivax Solutions St...
-
In the above animation, five points on the wave are considered for the explanation. The fully interactive applet is given below for you ...
-
Multiple Choice Questions - A Level Physics - electricity - Time: 40 minutes Created and Programmed by Vivax Solutions Star...
-
Denary to Binary Conversion Denary to binary conversion is a fundamental concept in computer science and digital electronics. It involves t...
-
Multiple Choice Questions - A Level Physics - Capacitors - Master capacitor concepts with this interactive A Level Physics quiz! Whether...
TOP CATEGORIES
- a level computer science (11)
- a level physics (43)
- gcse maths (30)
- gcse physics (14)
- general physics (11)
Featured Post
Labels
a level computer science
(11)
A Level Maths
(27)
a level physics
(43)
featured
(4)
GCSE Computer Science
(9)
gcse maths
(30)
gcse physics
(14)
general physics
(11)
math
(2)
physics
(2)
Blog Archive
-
▼
2022
(77)
-
▼
April
(7)
- Timed Multiple Questions Test for A Level Physics ...
- Challenging questions for in friction - for physic...
- Modelling with Differentiation for A Level Maths a...
- The dot product of two vectors: for A Level Furth...
- Simple Harmonic Motion of a liquid inside a U Tube
- Challenging questions for A Level Physics
- Chromatic Aberration
-
▼
April
(7)