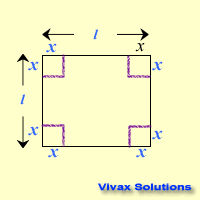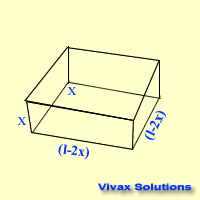
Four squares from the corners of a square plate are removed so that it can be turned into a open cubical box. Find the length of a square to be removed in terms of the length of the main square so that the volume of the box is a maximum.
Let the length of the plate be l and that of a small square be x.
If the volume is V,
V = x(l - 2x)2
= x(l2 - 4lx + 4x2)
= l2x - 4lx2 + 4x3
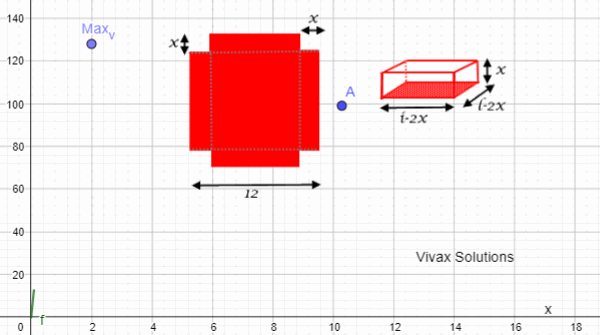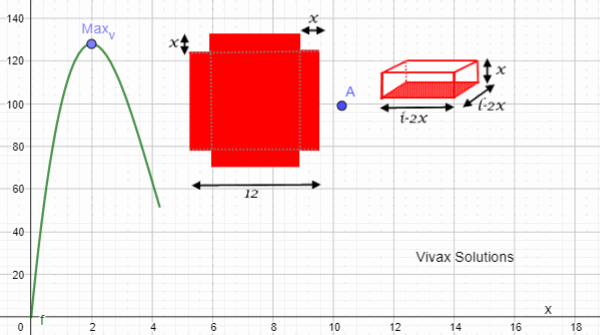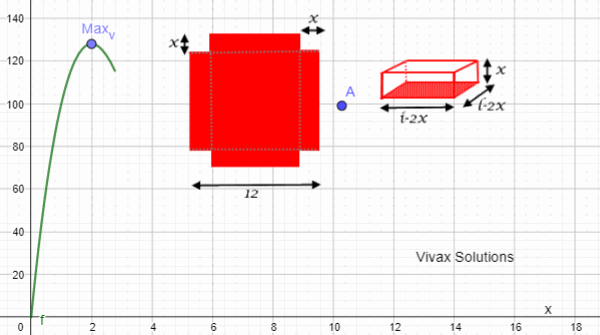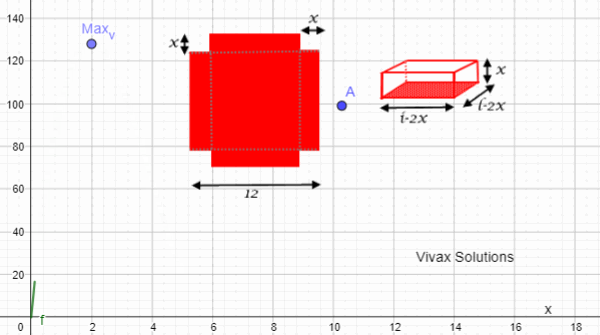
dV/dx = l2 - 8lx + 12x2
At the peak of the graph of V against x, dV/dx = 0
12x2 - 8lx + l2 = 0
x = 8l ± √ 64l2 - 48l2 / 24
x = 8l ± √ 16l2 / 24
x = 8l ± 4l / 24
x = l/2 or l/6
Since l/2 is not possible, x = l/6
Therefore, to maximize the volume, a square of side l/6 should be cut off from each corner of the plate.
If the length is 12 cm, the model is as follows:





0 comments:
Post a Comment