Vivax Solutions Blog

  The following example shows how to use lambda functions in Python. They are anonymous functions; they save quite a bit of code writing and in this context, very efficient. Lambda functions can easily be extend in OOP, Obeject Oriented Programming, too.

  Newton’s First Law of Motion An object is either at rest or moves at a constant speed in a straight line unless it is acted upon by an external force. Newton’s Second Law of Motion The rate of change of Momentum of an object is proportional to the force that caused it. In the above animation, the car is subjected to two forces: driving force, D, that acts forward and the resistive force, R, the combination of friction and drag. When D > R, there is a resultant force, F, acting on the car and according to the F = ma, there is a corresponding acceleration – Newton’s Second Law. When D = R, however, the resultant force, F, is zero. Therefore, according to F = ma, the acceleration is zero. As a result, the car continues to move at a constant velocity – in line with Newton’s First Law. Not only does the above animation illustrate Newton’s First and Second Laws of Motion, but also shows that the two laws are compatible. You can play with the animation here: Food fo

  The moving average, also known as the rolling average or running average, provides us with a value to make more meaningful predictions from a time-series; it will be clearer to you before the end of this tutorial how moving average can smooth out a data cure, while giving a more accurate picture for forecasts/predictions.  E.g. It takes into account a few successive data values and find an average, and then extends it to cover the whole time-series. It is done as follows: E.g. 1st 3-point moving average = (56 + 58 + 60)/3 = £ 58.00 2nd 3-point moving average = (58 + 60 + 59)/3 = £ 59.00 3rd 3-point moving average = (60 + 59 + 62 )/3 = £ 60.33 To learn the moving average interactively, please use this link.

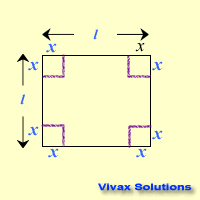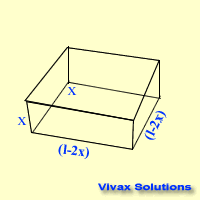
  Four squares from the corners of a square plate are removed so that it can be turned into a open cubical box. Find the length of a square to be removed in terms of the length of the main square so that the volume of the box is a maximum. Let the length of the plate be l and that of a small square be x. If the volume is V, V = x(l - 2x) 2 = x(l 2 - 4lx + 4x 2 ) = l 2 x - 4lx 2 + 4x 3 dV/dx = l 2 - 8lx + 12x 2 At the peak of the graph of V against x, dV/dx = 0 12x 2 - 8lx + l 2 = 0 x = 8l ± √ 64l 2 - 48l 2 / 24 x = 8l ± √ 16l 2 / 24 x = 8l ± 4l / 24 x = l/2 or l/6 Since l/2 is not possible, x = l/6 Therefore, to maximize the volume, a square of side l/6 should be cut off from each corner of the plate. If the length is 12 cm, the model is as follows:  

This is a jigsaw puzzle of Sir Isaac Newton, the legendary English physicist who contributed so much to the field of mathematics and physics.  It is fully interactive. Play and have fun.