An astronomical telescope is a refractiong telescope that consists of two convex lenses - the objective lens and the eyepiece. The objective lens gathers light from a distant object and the image formed, is viewed through the eyepiece. When the final image is formed in infinity, the rays enter the ey…
Monday, 31 January 2022
Sunday, 30 January 2022
Friday, 28 January 2022
Python Lambda Functions - anonymous functions
The following example shows how to use lambda functions in Python. They are anonymous functions; they save quite a bit of code writing and in this context, very efficient. Lambda functions can easily be extend in OOP, Obeject Oriented Programming, too.
Newton's Second and Third Laws of Motion in One Example
Newton’s First Law of Motion An object is either at rest or moves at a constant
speed in a straight line unless it is acted upon by an external force. Newton’s Second Law of Motion The rate of change of Momentum of an object is proportional
to the force that caused it. In the above animation, the car i…
Thursday, 27 January 2022
Moving Average
The moving average, also known as the rolling average or running average, provides us with a value to make more meaningful predictions from a time-series; it will be clearer to you before the end of this tutorial how moving average can smooth out a data cure, while giving a more accurate picture fo…
Wednesday, 26 January 2022
Differentiation: real life problem solving
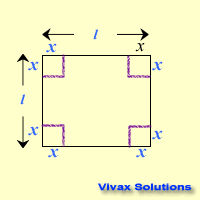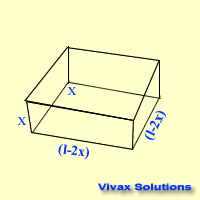
Four squares from the corners of a square plate are removed so that it can be turned into a open cubical box. Find the length of a square to be removed in terms of the length of the main square so that the volume of the box is a maximum. Let the length of the plate be l and that of a small square be…
Isaac Newton in a Jigsaw Puzzle - interactive play
This is a jigsaw puzzle of Sir Isaac Newton, the legendary English physicist who contributed so much to the field of mathematics and physics. It is fully interactive. Play and have fun.
Friday, 21 January 2022
The Redshift: star HD 94028 in stellar motion
This is the stellar motion of the star, HD-94028, in
space. The light emitted by the star is collected through a diffraction grating
to split it up into its various components, before being analysed. When the intensity of the hydrogen-alpha radiation
plotted against the wavelength, the above graph c…
Subscribe to:
Posts (Atom)
Popular Posts
-
Multiple Choice Questions - A Level Physics and Mechanics - Time: 40 minutes Created and Programmed by Vivax Solutions St...
-
In the above animation, five points on the wave are considered for the explanation. The fully interactive applet is given below for you ...
-
Multiple Choice Questions - A Level Physics - electricity - Time: 40 minutes Created and Programmed by Vivax Solutions Star...
-
The above shows how a column of liquid of density ρ can be made to oscillate while undergoing SHM, simple harmonic motion. Wh...
-
Multiple Choice Questions - A Level Physics - Capacitors - Master capacitor concepts with this interactive A Level Physics quiz! Whether...
TOP CATEGORIES
- a level computer science (11)
- a level physics (42)
- gcse maths (28)
- gcse physics (13)
- general physics (11)
Labels
a level computer science
(11)
A Level Maths
(27)
a level physics
(42)
featured
(4)
GCSE Computer Science
(9)
gcse maths
(28)
gcse physics
(13)
general physics
(11)
math
(1)
Blog Archive
-
▼
2022
(77)
-
▼
January
(8)
- Astronomical Telescope Explained - with interactiv...
- The jigsaw of the physicst, born in Oxford died in...
- Python Lambda Functions - anonymous functions
- Newton's Second and Third Laws of Motion in One Ex...
- Moving Average
- Differentiation: real life problem solving
- Isaac Newton in a Jigsaw Puzzle - interactive play
- The Redshift: star HD 94028 in stellar motion
-
▼
January
(8)