Concave, convex functions and points of inflection

-

 

Convex, concave functions and points of inflection

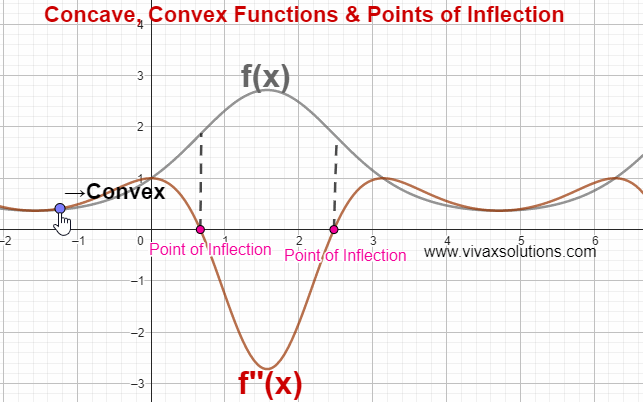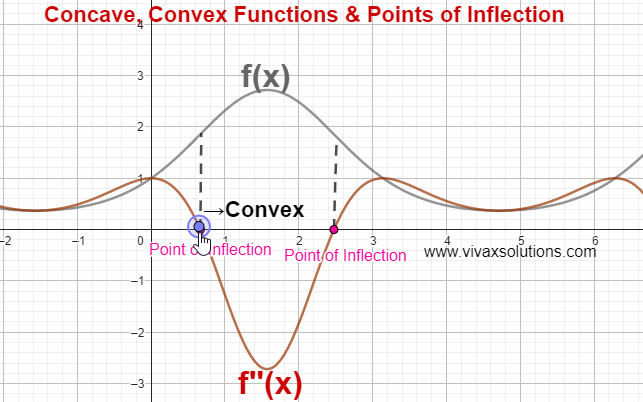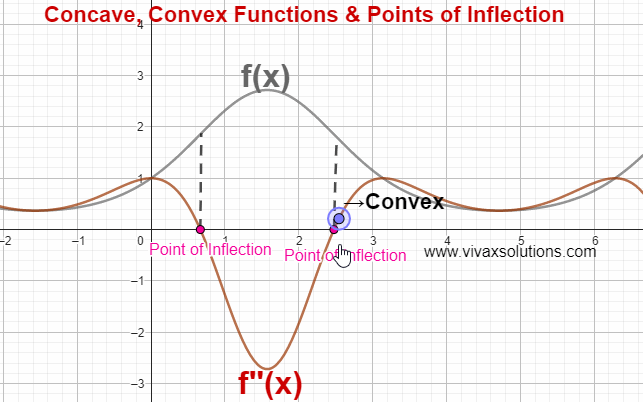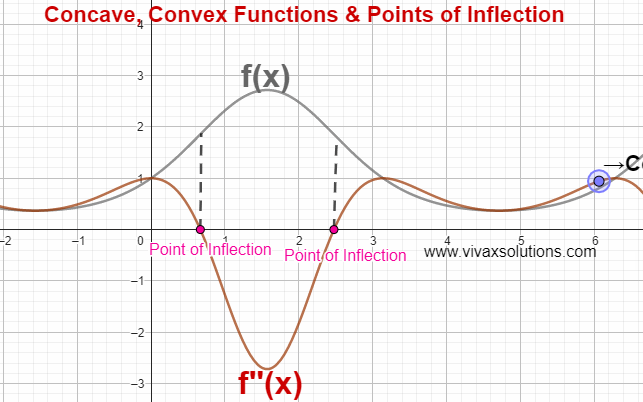
Concave functions

If f''(x) ≤ 0 in a given interval of x, the function is said to be concave.

Convex functions

If f''(x) ≥ 0 in a given interval of x, the function is said to be convex.

Point of Inflection

The point at which a curve changes being concave to convex or vice versa is called a point of inflection.

E.g.
f(x) = x3 - 2x² + 5x - 4
f'(x) = 3x² - 4x + 5
f''(x) = 6x - 4

At the point of inflection,
f''(x) = 0
6x - 4 = 0
x = 2/3 = 0.67
There is a point of inflection at x = 0.67.

If x = 0.6
f''(0.6) = 3.6 - 4 = -0.4
f''(0.6) < 0 - the function is concave.

If x = 0.8
f''(0.8) = 4.8 - 4 = 0.8
f''(0.8) > 0 - the function is convex.

In the above simulation, there are two points of inflection. The simulation can be practised interactively here; just move the point gently to see the change.

 

Points of inflection on the Bell Curve - Normal Distribution

There are two points of inflection on the bell curve. You can practise the following simulation interactively to understand it.

 

Comments

Post a Comment

Popular posts from this blog

Phase Difference between Two Points on a Wave and Path Difference Explained - interactive

-
Image
  In the above animation, five points on the wave are considered for the explanation.  The fully interactive applet is given below for you to practise. The phase of a point implies its direction of vibration on a wave. For example, both points A and E vibrate exactly the same way are said to be in phase: when A goes up so does B; the phase difference is either 0 0 or 360 0 . If you consider the motion of points A and C, on the other hand, when A goes down C goes up or vice versa. Therefore, A and C are said to be out of phase; the phase difference is 180 0 . That means the phase difference between two points on a wave - or two waves for that matter - can take any value between 0 0 and 360 0 .  The phase difference between points A and B, for instance, is 90 0 . From the above examples, it is clear there is a connection between the path difference between two points - or two waves - and phase difference. It is as follows: Phase difference = (path difference / wavelength) x 360 φ = x
Read more

Frequency Amplitude and Wavelength of a Transverse Wave - simulation

-
Image
Waves A wave carries energy from a point to another point in a medium / vacuum without the movement of the particles along with it. In the above animation, the wave moves from the left to the right; the particles, however, just vibrate vertically without moving along with the wave. Transverse Waves If the direction of the wave is perpendicular to the vibration of particles, it is called a transverse wave. E.g. Water waves, radio waves, microwaves Amplitude The maximum displacement of a particle in a wave is called amplitude. Intensity / loudness The intensity / loudness of a wave is proportional to the square of the amplitude. The greater the amplitude, the greater the intensity / loudness. Amplifier This is what an amplifier does: it increases the amplitude of an input signal, which in turn leads to the increased loudness or intensity. Frequency  - f The number of cycles of a wave that passes through a point in a unit time is called frequency. Wavelength  - λ The distance between
Read more