When it comes to differentiating the functions of sin x and cos x, we need to use two fractions of the functions in question, when the variable approaches zero must be considered. They are as follows:
lim sin (x) / x, as x → 0
lim (cos x - 1) / x as x → 0
Based on the above, sin x and cos x can be differentiated as follows:
y = sin x → dy/dx = cos x
y = cos x → dy/dx = - sin x
y = tan x → dy/dx = sec² x
Differentiation of sine function
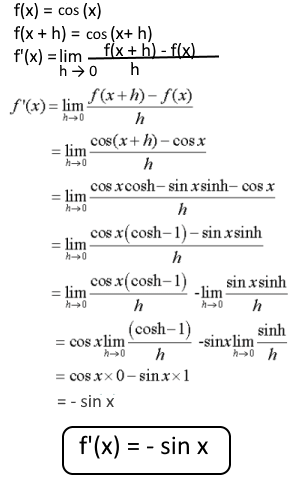
0 comments:
Post a Comment