Iteration
If f(x) =0, it can be rearranged in the form of x = g(x), where both f(x) and g(x) are functions of x. Then x = g(x) is said to be in iterative form.
E.g.
x² - x - 5 = 0
x² = x + 5
xn+1 = √(xn + 5) - f(x) = 0 in iterative form
If xn is known, xn+1 can be calculated.
The above is not the only iterative form, though: two more iterative forms from can be derived from it; every form, however, may not produce the required result! it's important to choose the correct form.
In order to start the process, the initial value, x0, is usually given.
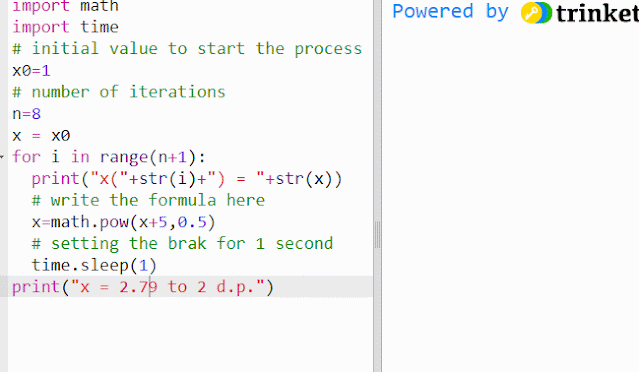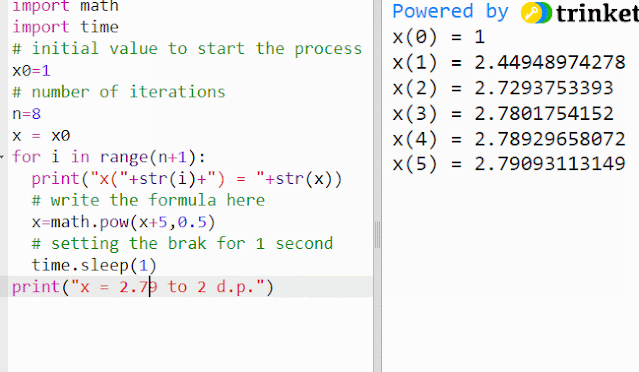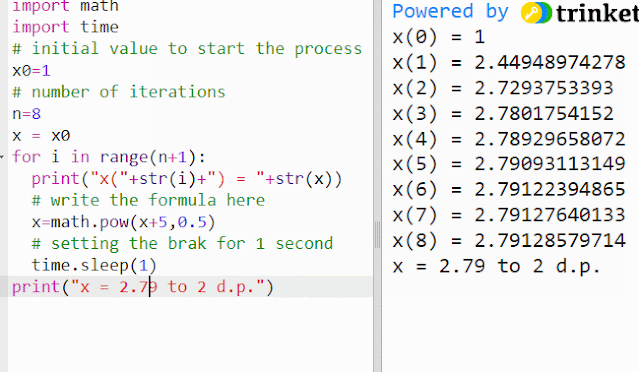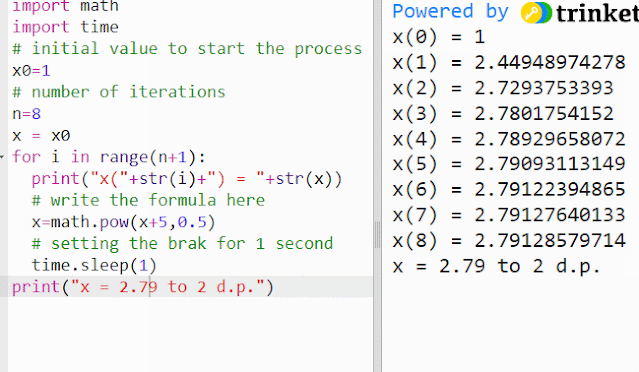
When the values of x becomes almost constant, the last value can be approximated as the solution or the root of the equation, to an appropriate significant level.
For example, the above simulation shows how the process can be triggered off by taking x0 = 1.
You can practise it here interactively; just change the value of x0 and run the simulation:





0 comments:
Post a Comment