Maximizing the power of load in an electric circuit

-

Maximizing the power of load in a circuit: R = r


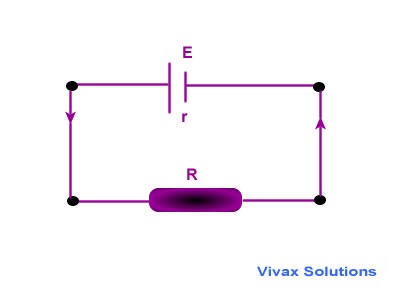
Let the EMF, internal resistance, load and the current of a circuit be E, r, R and I respectively.

Maximising the power of a load - external resistance = internal resistance


E = I(R + r)

I = E/(R + r)

The power of the load, the external resistor in this case, is as follows:

P = VI

P = E2R/(R + r)2
Let's differentiate P with respect to R
dP/dR = E2/ / (R + r)2 - 2E2R / (R + r)3
When P is maximum, 

dP/dR = 0
E2/ / (R + r)2 - 2E2R / (R + r)3 = 0
R + r = 2R
R = r

As you can see, the power is maximum, when the external resistance is equal to the internal resistance of the battery or cell.

 

 

E.g. 

R = r

E = 12V R = 6 r = 6

Power = (12/12)2 X 6 = 6W

R > r

E = 12 R  = 12 r = 6

Power = (12/18)2 X 12 = 5.3W

R < r

E = 12 R = 4 r = 6

Power = (12/10)2 X 4 = 5.7 W

You can practise the above with the following interactive simulation:


 

 

For a comprehensive tutorial on electricity, for GCSE, IGCSE, IB, A Level,  GCE OL and GCE AL, please use this link.

Comments

Post a Comment

Popular posts from this blog

Phase Difference between Two Points on a Wave and Path Difference Explained - interactive

-
Image
  In the above animation, five points on the wave are considered for the explanation.  The fully interactive applet is given below for you to practise. The phase of a point implies its direction of vibration on a wave. For example, both points A and E vibrate exactly the same way are said to be in phase: when A goes up so does B; the phase difference is either 0 0 or 360 0 . If you consider the motion of points A and C, on the other hand, when A goes down C goes up or vice versa. Therefore, A and C are said to be out of phase; the phase difference is 180 0 . That means the phase difference between two points on a wave - or two waves for that matter - can take any value between 0 0 and 360 0 .  The phase difference between points A and B, for instance, is 90 0 . From the above examples, it is clear there is a connection between the path difference between two points - or two waves - and phase difference. It is as follows: Phase difference = (path difference / wavelength) x 360 φ = x
Read more

Frequency Amplitude and Wavelength of a Transverse Wave - simulation

-
Image
Waves A wave carries energy from a point to another point in a medium / vacuum without the movement of the particles along with it. In the above animation, the wave moves from the left to the right; the particles, however, just vibrate vertically without moving along with the wave. Transverse Waves If the direction of the wave is perpendicular to the vibration of particles, it is called a transverse wave. E.g. Water waves, radio waves, microwaves Amplitude The maximum displacement of a particle in a wave is called amplitude. Intensity / loudness The intensity / loudness of a wave is proportional to the square of the amplitude. The greater the amplitude, the greater the intensity / loudness. Amplifier This is what an amplifier does: it increases the amplitude of an input signal, which in turn leads to the increased loudness or intensity. Frequency  - f The number of cycles of a wave that passes through a point in a unit time is called frequency. Wavelength  - λ The distance between
Read more